If you want to break into cutting-edge AI, this course will help you do so.
Neural Networks and Deep Learning
All the courses
Course’s information
👉 Check Comparison of activation functions on wikipedia.
Suppose $g(z)=z$ (linear)
$$ \begin{aligned} a^{[1]} &= g(z^{[1]} = z^{[1]}) = w^{[1]}x + b^{[1]} \quad \text{(linear)} \\ a^{[1]} &= g(z^{[2]} = z^{[2]}) = w^{[2]}a^{[1]} + b^{[2]} \\ &= (w^{[2]}w^{[1]})x + (w^{[2]}b^{[1]} + b^{[2]}) \quad \text{(linear again)}. \end{aligned} $$
You might not have any hidden layer! Your model is just Logistic Regression, no hidden unit! Just use non-linear activations for hidden layers!
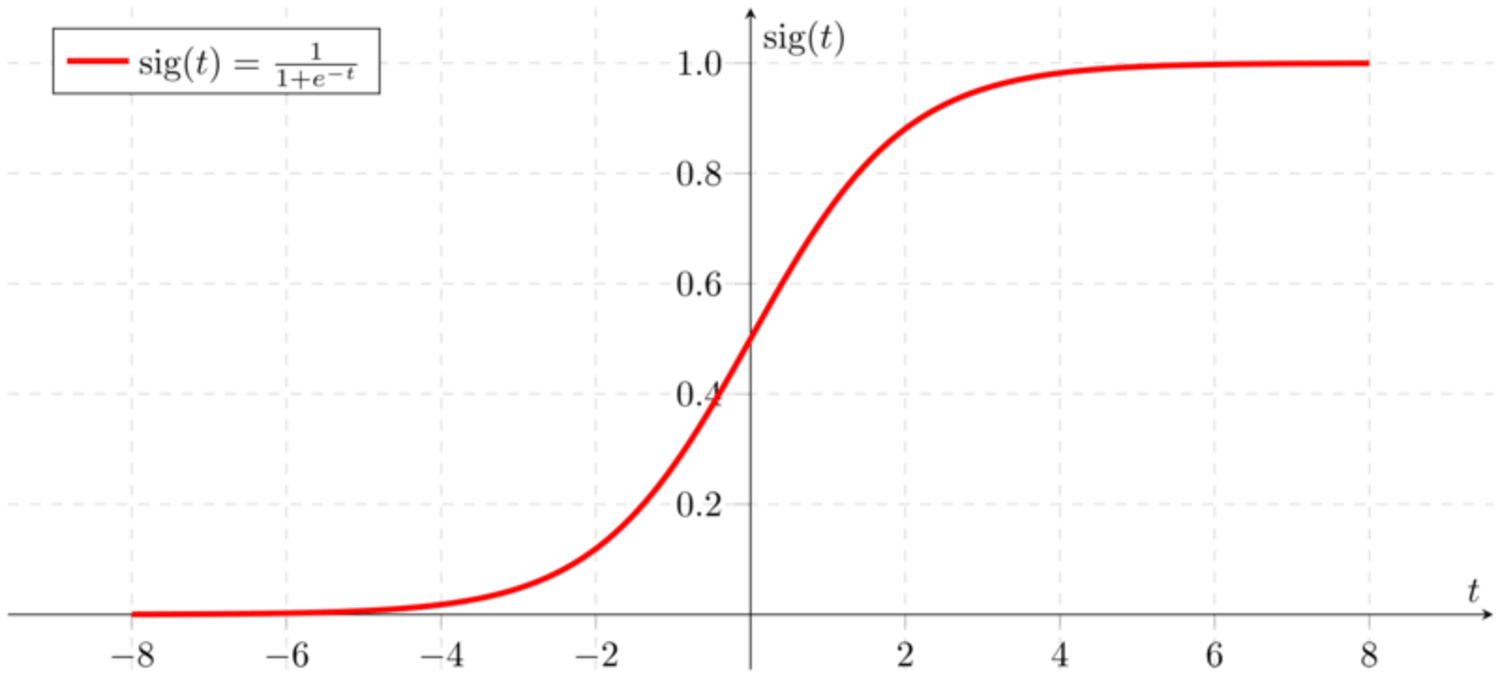
$$ \begin{aligned} \sigma(z) &= \dfrac{1}{1+e^{-z}} \\ \sigma(z) &\xrightarrow{z\to \infty} 1 \\ \sigma(z) &\xrightarrow{z\to -\infty} 0 \\ \sigma'(x) &= \sigma(x) (1 - \sigma(x)) \end{aligned} $$

Signmoid function graph on Wikipedia.
import numpy as np
import numpy as np
def sigmoid(z):
return 1 / (1+np.exp(-z))
def sigmoid_derivative(z):
return sigmoid(z)*(1-sigmoid(z))
The output of the softmax function can be used to represent a categorical distribution – that is, a probability distribution over K different possible outcomes.
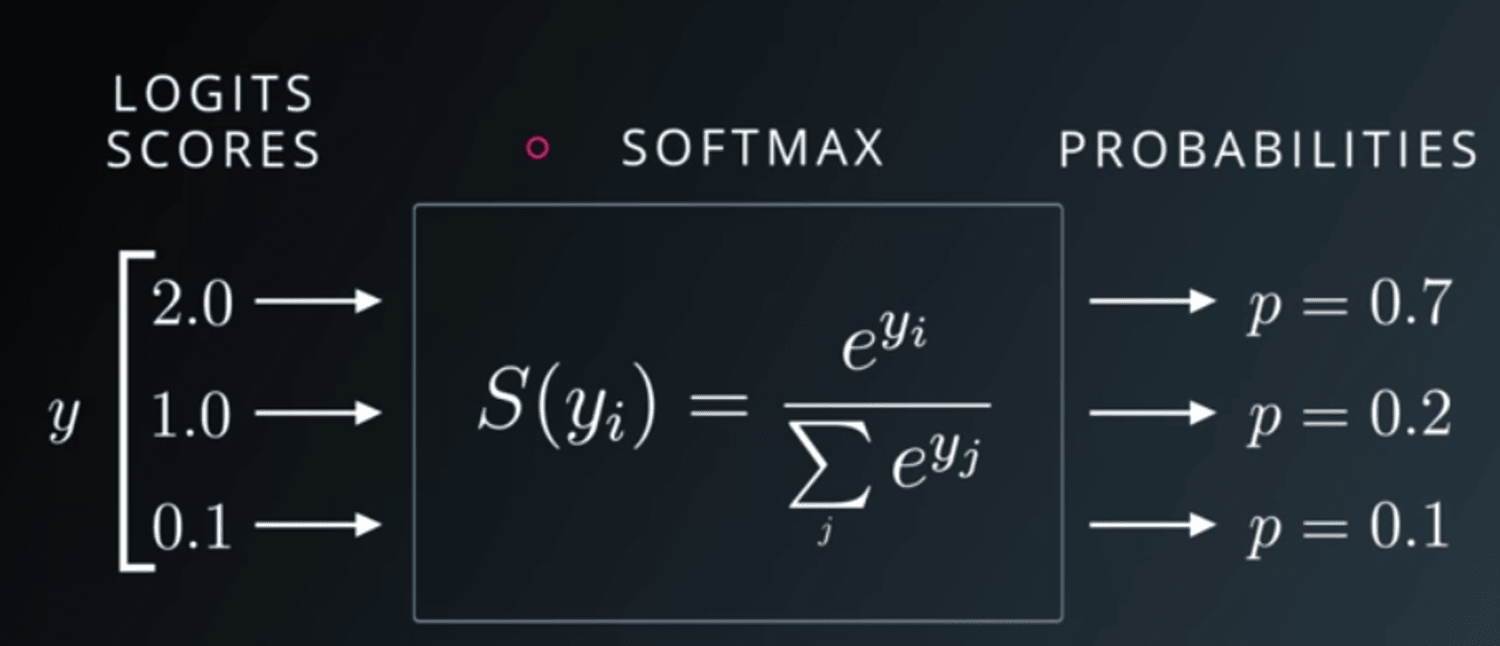
Udacity Deep Learning Slide on Softmax
$$ \sigma (\mathbf {z} ){i}={\frac {e^{z{i}}}{\sum_ {j=1}^{K}e^{z_{j}}}}{\text{ for }}i=1,\dotsc ,K{\text{ and }}\mathbf {z}\in \mathbb {R} ^{K} $$
def softmax(x):
z_exp = np.exp(z)
z_sum = np.sum(z_exp, axis=1, keepdims=True)
return z_exp / z_sum